常见的算术表达式，称为中缀表达式，例如：

1
5 + ( 6 – 4 / 2 ) * 3

波兰表达式

波兰表达式也称为前缀表达式，以上面的例子为例，其波兰表达式为：

1
+ 5 * - 6 / 4 2 3

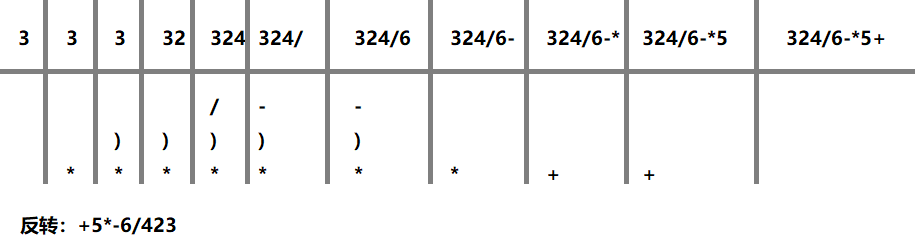
中缀表达式转换前缀表达式的操作过程为：

（1）首先设定一个操作符栈，自右向左顺序扫描整个中缀表达式：

  • 如果是操作数，则直接归入前缀表达式；

  • 如果是括号：如果是右括号，则直接将其入栈；如果是左括号，则将栈中的操作符依次弹栈，归入前缀表达式，直至遇到右括号，将右括号弹栈，处理结束；

  • 如果是其他操作符，则检测栈顶操作符的优先级与当前操作符的优先级关系，如果栈顶操作符优先级大于当前操作符的优先级，则弹栈，并归入前缀表达式，直至栈顶操作符优先级小于等于当前操作符优先级，这时将当前操作符压栈。

（2）当扫描完毕整个中缀表达式后，检测操作符栈是否为空，如果不为空，则依次将栈中操作符弹栈，归入前缀表达式。

（3）最后，将前缀表达式翻转，得到中缀表达式对应的前缀表达式。

逆波兰表达式

逆波兰表达式也称为后缀表达式，以上面的例子为例，其逆波兰表达式为：

1
5 6 4 2 / - 3 * +

中缀表达式转换后缀表达式的操作过程为：

（1）自左向右顺序扫描整个中缀表达式；

  • 如果当前元素为操作数，则将该元素直接存入到后缀表达式中；

  • 如果当前元素为“(”，则将其直接入栈；如果为“)”，则将栈中的操作符弹栈，并将弹栈的操作符存入到后缀表达式中，直至遇到“(”，将“(”从栈中弹出，并不将其存入到后缀表达式中；

  • 如果是其他操作符，如果其优先级高于栈顶操作符的优先级，则将其入栈，如果是小于或低于站定操作符优先级，则依次弹出栈顶操作符并存入后缀表达式中，直至遇到一个栈顶优先级小于当前元素优先级时或者栈顶元素为“(”为止，保持当前栈顶元素不变，并将当前元素入栈；

（2）当扫描完毕整个中缀表达式后，检测操作符栈是否为空，如果不为空，则依次将栈中操作符弹栈，归入后缀表达式。

下面程序演示如何将一个中缀表达式转换为后缀表达式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * 中缀表达式 -- >逆波兰表达式
 * @author jitwxs
 * @since 2018/10/18 16:39
 */
public static String niBoLan(String src) {
    Stack<Character> stack = new Stack<>();

    StringBuilder sb = new StringBuilder();
    char tmp;

    for (int i = 0; i < src.length(); i++) {
        char c = src.charAt(i);

        if (Character.isDigit(c)) { // 如果是数字，直接输出
            sb.append(c);
        } else if (c == '(') { // 如果是左括号，直接入栈
            stack.push(c);
        } else if (c == ')') { // 如果是右括号，全部出栈输出，直到遇见左括号【左括号不输出】
            while ((tmp = stack.pop()) != '(') {
                sb.append(tmp);
            }
        } else {
            // 如果是操作符，如果操作符比栈顶小，将栈顶元素出栈输出，直到操作符大于等于栈顶。最后将操作符入栈。
            while (!stack.empty() && getPriority((tmp = stack.peek())) > getPriority(c)) {
                sb.append(tmp);
                stack.pop();
            }
            stack.push(c);
        }
    }

    // 输出结束后，如果操作符栈非空，全部出栈
    while (!stack.empty()) {
        sb.append(stack.pop());
    }

    return sb.toString();
}

/**
 * 获取优先级
 * @author jitwxs
 * @since 2018/10/18 16:42
 */
public static int getPriority(Character op) {
    switch(op){
        case '+':
        case '-':
            return 1;
        case '*':
        case '/':
            return 2;
        default:
            return 0;
    }
}

波兰表达式计算

  1. 对前缀表达式从后向前扫描，设定一个操作数栈，如果是操作数，则将其直接入栈。

  2. 如果是操作符，则从栈中弹出操作符对应的操作数进行运算，并将计算结果压栈。

  3. 直至从右到左扫描完毕整个前缀表达式，这时操作数栈中应该只有一个元素，该元素的值则为前缀表达式的计算结果。

逆波兰表达式计算

  1. 从左到右顺序扫描整个后缀表达式；

  2. 如果是操作数，则将该操作数压入到栈中；

  3. 如果是操作符，则从栈中弹出对应的操作数，注意操作数的顺序；根据操作符进行运算，并将结果重新压入到栈中；

  4. 直至将整个栈扫描完毕；

  5. 如果后缀表达式是合法的，则扫描完毕后，栈中只有一个元素，该元素的值即为后缀表达式的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * 计算逆波兰表达式数值
 * @author jitwxs
 * @since 2018/10/18 17:18
 */
public static Integer calNiBoLan(String str) {
    Stack<Integer> numStack = new Stack<>();
    
    for(int i = 0; i<str.length(); i++) {
        char c = str.charAt(i);
        if(Character.isDigit(c)) {
            numStack.push(c - '0');
        } else {
            int b = numStack.pop();
            int a = numStack.pop();
            int tmp;
            switch (c) {
                case '+':
                    tmp = a + b;
                    break;
                case '-':
                    tmp = a - b;
                    break;
                case '*':
                    tmp = a * b;
                    break;
                case '/':
                    tmp = a / b;
                    break;
                default:
                    tmp = 0;
                    break;
            }
            numStack.push(tmp);
        }
    }

    return numStack.pop();
}

总结

（1）中缀转前缀/后缀

类别 中缀转前缀 中缀转后缀
栈 操作符栈 操作符栈
扫描顺序 从右到左 从左到右
遇到操作数 直接归入 直接归入
遇到右括号 直接入栈 将栈中操作符依次弹栈，归入，直至遇到左括号，将左括号弹栈，处理完毕
遇到左括号 将栈中操作符依次弹栈，归入，直至遇到右括号，将右括号弹栈，处理完毕 直接入栈
遇到其他操作符 检测栈顶操作符优先级与当前操作符优先级关系，如果栈顶大于当前，则出栈，归入，直至栈顶小于等于当前，并将当前操作符入栈 检测栈顶与当前优先级关系，如果栈顶大于等于当前则出栈，归入，直至栈顶小于当前，并将当前操作符入栈
操作符栈中的优先级 从栈底到栈顶操作优先级：非递减。即：栈顶可以大于或等于下面的 从栈底到栈顶优先级：递增。即：栈顶必须大于下面的
是否翻转 翻转 无需翻转

（2）前缀/后缀表达式计算

类别 前缀表达式计算 后缀表达式计算
扫描顺序 从右到左 从左到右
栈 操作数栈 操作数栈
遇到操作数时 压栈 压栈
遇到操作符时 出栈 出栈
出栈的顺序 先弹出操作数a，后弹出b 先弹出操作数b，后弹出a
结果 操作数栈中唯一元素的值 操作数栈中唯一元素的值