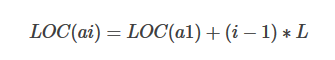2.1 线性表的概念和运算

2.1.1 线性表的概念

线性表是 n (n≥0) 个类型相同的数据元素组成的有限序列。其中数据元素的个数n为线性表的长度，当n=0时称为空表。

对于非空的线性表，有且仅有一个开始结点和一个终端结点。

开始结点没有直接前趋，有且仅有一个直接后继；终端结点没有直接后继，有且仅有一个直接前趋；其余任何结点有且仅有一个直接前趋和一个直接后继。

2.1.2 线性表的特点

（1）同一性：线性表由同类数据元素组成，每一个ai必须属于同一数据对象。
（2）有穷性：线性表由有限个数据元素组成，表长度就是表中数据元素的个数。
（3）有序性：线性表中相邻数据元素之间存在着序偶关系 <ai,ai+1>< a_i, a_{i+1} > 。

2.1.3 线性表的计算

(1) 置空表 SETNULL(L) ：将线性表L置为空表。

(2) 求长度 LENGTH(L) ：返回是线性表L中结点的个数。

(3) 取结点 GET(L, i ) ：当1 ≤ i ≤ LENGTH(L)时，返回线性表L中的第 i 个结点，否则返回NULL。

(4) 定位 LOCATE(L, x) ：当线性表L中存在一个值为x的结点时，结果是该结点的位置；若表L中存在多个值为x的结点，则返回首次找到的结点位置；若表L中不存在值为x的结点，则返回一个特殊值表示值为x的结点不存在。

(5) 插入 INSERT(L, x, i) ：在线性表L的第i个位置插入一个值为x的新结点。这里1 ≤ i ≤ n+1，n是原表L的长度。

(6) 删除 DELETE(L, i) ：删除线性表L的第i个结点。这里1 ≤ i ≤ n，n是原表L的长度。

2.2 线性表的顺序存储

2.2.1 定义

把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。简言之，逻辑上相邻，物理上也相邻。

2.2.2 顺序存储方法

用一组地址连续的存储单元依次存储线性表的元素，可通过数组来实现。

2.2.3 地址计算

设首元素 a1a_1 的存放地址为LOC(a1)（称为首地址），设每个元素占用存储空间（地址长度）为L字节，则地址计算公式：

2.2.4 结构定义：

1
2
3
4
5
6
7
#define  MAXSIZE 1024  //线性表的最大长度
typedef int datatype;     //线性表数据元素类型
typedef  struct 
{
    datatype  data[MAXSIZE];
    int  last;   //指示线性表的终端结点在表中的下标值
}sequenlist;

2.3 线性表的链式存储

2.3.1 概念

用一组任意的存储单元存储线性表的数据元素，利用指针实现了用不相邻的存储单元存放逻辑上相邻的元素，每个数据元素 aia_i ，除存储本身信息外，还需存储其直接后继的信息。

链式存储结构分为单链表、循环单链表、双向链表和静态链表。

  • 从链接方式看，可分为单链表、循环链表和双向链表。

  • 从实现角度看，可分为动态链表和静态链表。

2.3.2 头指针、头节点、开始节点

头指针是指向链表中第一个结点（或为头结点或开始结点）的指针，单链表可由一个头指针唯一确定。

头结点是在链表的开始结点之前附设的一个结点；数据域内只放空表标志和表长等信息；

开始结点是指链表中存储线性表第一个数据元素a1的结点。

2.3.3 空表的表示

无头结点时，当头指针的值为空时表示空表；

有头结点时，当头结点的指针域为空时表示空表。

2.3.4 单链表

2.3.4.1 结构定义

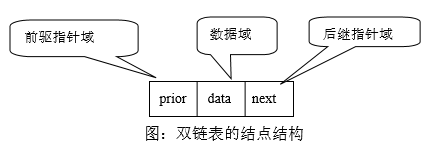
链表中的结点包括数据域和指针域。数据域data用来存储结点的值，指针域next用来存储节点本身的信息，邻接关系由后继指针指示其位置。

1
2
3
4
5
typedef int datatype;     //线性表数据元素类型
typedef struct node {
     datatype     data;  //数据域
     struct node   *next;  //指针域
} linklist;
2.3.4.2 单链表操作

（1）查找

1
2
3
4
5
6
7
8
9
10
void findValue(Linklist *head ,int x){
    Linklist *t;
    t = head->next;
    while(t!=NULL && t->data !=x)
        t=t->next;
    if(t->data == x)
        printf("成功找到\n");
    else
        printf("没有找到\n");
}

（2）插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void insert(Linklist *head,int x){
    Linklist *t,*p;
    p = (Linklist*)malloc(sizeof(Linklist));
    p->data = x;
    t = head;
    while(t->next != NULL && t->next->data < x){
        t = t->next;
    }
    if(t == head){
        p->next = head->next;
        head->next = p;
    }else if(t->next == NULL){
        t->next = p;
        p->next = NULL;
    }else{
        p->next = t->next;
        t->next = p;
    }
}

（3）删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void dele(Linklist *head){
    Linklist p ,q;
    p=head;
    while (p->next !=NULL){
        if (p->data !=p->next->data){
            p=p->next;
        }
        else{ 
            q=p->next; 
            p->next=q->next; 
            free(q);
        }
    }
}

（4）逆置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void reverse(Linklist *head){
    Linklist *s,*t,*p; 
    p = head; 
    s = p->next; 
    while(s->next != NULL) { 
        t = s->next; 
        s->next = p; 
        p = s;
        s = t;
    }
    s->next = p;
    head->next->next = NULL;
    head->next = s;
}

2.3.5 循环单链表

2.3.5.1 概念

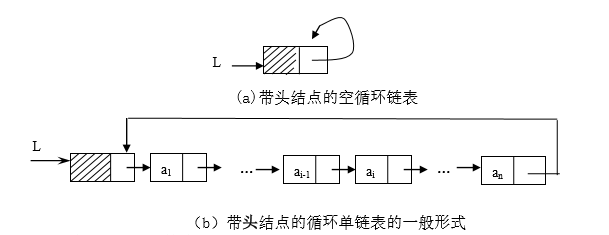
单链形式的循环链表结构是首尾相接的单链表，即最后一个结点的指针指 向链表的表头结点或第一个结点。

判别当前结点 p 是否为循环单链表 L 的表尾结点的判别条件： p->next!=L ，即 p->next 是否指回到头，与一般单链表 p->next 是否为 NULL 不同。

在循环单链表中，也可只设置一个头结点，这样，空循环链表仅由一个自成循环的头结点表示。

循环单链表

判断循环空链表的条件是头结点的指针域指向自己,即 head->next = =head。

2.3.5.2 合并算法

有两个带头结点的循环单链表 LA、LB，设计算法，将两个循环单链表合并为一 个循环单链表，其头指针为 LA。

（1）思想

  • 遍历两链表找表尾。

  • 将第一表尾链接第二表头，将第二表尾链接第一表头。

（2）步骤

①设置指针 p，q 从头遍历查找两链表的表尾；

②修改第一表的尾指针，使其指向第二表的头结点；

③修改第二表的尾指针，使其指向第一表的头结点；

（3）实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
LinkList merge_1(LinkList LA,LinkList LB) {
    /*此算法将两个采用头指针的循环单链表的首尾连接起来*/ 
    Node *p, *q; 
    p=LA; 
    q=LB; 
    
    /*找到表 LA 的表尾，用 p 指向它*/
    while (p->next!=LA){
         p=p->next;
    } 
    
    /*找到表 LB 的表尾，用 q 指向它*/
    while (q->next!=LB){
         q=q->next;
    }  
    
    q->next=LA; /*修改表 LB 的尾指针，使之指向表 LA 的头结点*/ 
    p->next=LB->next; /*修改表 LA的尾指针，使之指向表 LB 中的第一个结点*/ 
    
    free(LB); 
    
    return(LA); 
}

2.3.6 双向链表

2.3.6.1 概念

循环单链表的出现，虽然能够实现从任一结点出发沿着链能找到其前趋结 点，但时间耗费是 O(n)O(n)。

如果希望从表中快速确定某一个结点的前趋，另一个解决方法就是在单链表 的每个结点里再增加一个指向其前趋的指针域 prior。这样形成的链表中就有 两条方向不同的链，我们称之为双向链表。

2.3.6.2 结构定义
1
2
3
4
typedef struct DNode { 
    ElemType data； 
    struct DNode *prior，*next； 
}DNode, * DoubleList； 

双向链表

  • 双向链表也是由头指针唯一确定的

  • 增加头结点能使双链表的某些运算变得方便

  • 由于在双向链表中既有前向链又有后向链，寻找任一个结点的直接前驱结点 与直接后继结点变得非常方便

  • 设指针p指向双链表中某一结点，则有下式成立：p->prior->next = p = p->next->prior

  • 在双向链表中，那些只涉及后继指针的算法，如求表长度、取元素、元素定 位等，与单链表中相应的算法相同，但对于前插和删除操作则涉及到前驱和后继两个方向的指针变化，因此与单链表中的算法不同

2.3.6.3 双向链表的前插操作

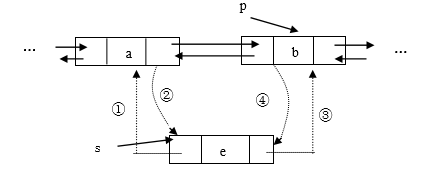
欲在双向链表第 i 个结点之前插入一个的新的结点，则指针的 变化情况如图所示：

双向链表的前插操作

①：s->prior=p->prior;
②：p->prior->next=s;
③：s->next=p;
④：p->prior=s;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int DlinkIns(DoubleList L,int i,ElemType e){ 
    DNode  *s,*p; 
      
      … /*先检查待插入的位置 i 是否合法（实现方法同单链表的前插操作）*/ 
     … /*若位置 i 合法，则找到第 i 个结点并让指针 p 指向它*/ 
    
    s=(DNode*)malloc(sizeof(DNode)); 
    
    if (s){ 
        s->data=e;   
          s->prior=p->prior;
        p->prior->next=s;
        s->next=p;
        p->prior=s;
        return TRUE; 
     }else 
         return FALSE; 
}

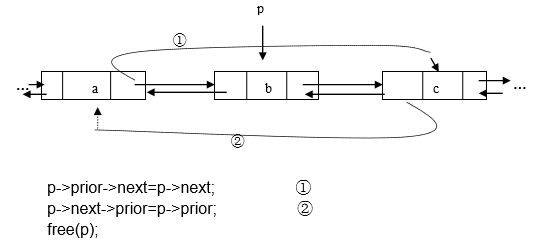
2.3.6.4 双向链表的删除操作

欲删除双向链表中的第 i 个结点，则指针的变化情况如图所示：

双向链表的删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
int DlinkDel(DoubleList L,int i,ElemType *e){   
    DNode  *p;
    
    … /*先检查待插入的位置 i 是否合法（实现方法同单链表的删除操作）*/ 
    … /*若位置 i 合法，则找到第 i 个结点并让指针 p 指向它*/
    
    p->prior->next=p->next;
    p->next->prior=p->prior;
    
    free(p);
    
    return TRUE;
}
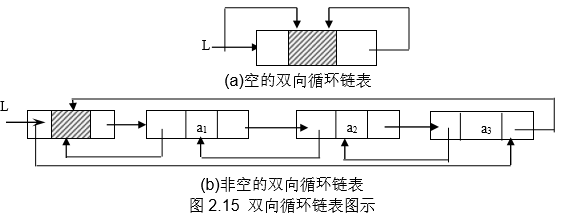
2.3.6.5 双向循环链表

双向循环链表

2.4 存储结构比较

存储密度：是指终点信息所占存储空间与整个结点的存储量之比。

2.4.1 顺序表和链表的比较

2.4.1.1 空间考虑

顺序表存储是静态分配，程序执行前须定义存储规模。

静态链表是静态分配，同时存在若干个结点类型相同的链表，可共享空间。

动态链表是动态分配，只要存内存空间尚有空闲就不会产生溢出。

顺序表存储密度等于1，而链表的存储密度小于1。

2.4.1.2 时间考虑

顺序表是一种随机存储结构，对表中任一结点都可以在 O(1)O(1) 时间内直接地存取。但是要进行插入或删除操作时，平均要移动一半的结点，时间复杂度达到了 O(n)O(n)。因此，顺序表适合做查找这样的静态操作。

单链表在做插入和删除操作时，只用修改挂链，不需要移动元素，适合动态变化。但是查找元素需要从头指针顺着链栈才能找到。因此，适合做插入、删除这样的动态操作。

2.4.1.3 语言考虑

有些语言环境支持指针，因此可以用链表形式。有些语言环境不支持，只能用静态链表来模拟。

2.4.2 线性表链式存储方式的比较

链表名称 找表头结点 找表尾结点 找P结点前驱结点
带头节点单链表L L->next，时间耗费 O(1)O(1) 一重循环，时间耗费 O(n)O(n) 顺 P 结点的 next 域无法找到 P 结点 的前驱
带头结点循环单链表（头指针）L L->next，时间耗费O(1) 一重循环，时间耗费O(n) 顺 P 结点的 next 域可以找到 P 结点 的前驱，时间耗费 O(n)O(n)
带尾指针的循环单链表R R->next，时间耗费 O(1)O(1) R，时间耗费 O(1)O(1) 顺 P 结点的 next 域可以找到 P 结点的前驱，时间耗费 O(n)O(n)
带头结点双向循环链表L L->next，时间耗费 O(1)O(1) L->prior，时间耗费 O(1)O(1) P->prior，时间耗费 O(1)O(1)

2.5 例题

2.5.1 例1

一个一维数组M，下标的范围是0到9，每个数组元素用相邻的5个字节存储。存储器按字节编址，设存储数组元素M[O]的第一个字节的地址是98，则M[3]的第一个字节的地址是_____。

113

2.5.2 例2

在一个长度为n的顺序表中向第i个元素（1≤i≤n+1）之前插入一个新元素时，需要向后移动_________个元素（或删除第i个元素，需要向前移动________个元素）。

n-i+1 ; n-i

2.5.3 例3

在单链表中，若p结点不是末尾结点，在其前或后插入s结点或删除结点的操作是？
解：

在其前插入s结点：s->next= p->next ; p->next=s; t=p->data; p->data=s->data ; s->data= t ;
在其后插入s结点：s->next=p->next; p->next=s;
删除其前结点：需要利用遍历
删除其后结点：q = p->next; p->next=q->next; free(q);
删除自身接结点：q=p->next; p->data= q->data ; p->next=q->next ; free(q);

2.5.4 例4

在线性表的下列存储结构中，读取指定序号的元素花费时间最少的是_______。

顺序结构