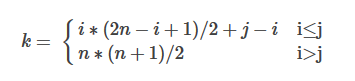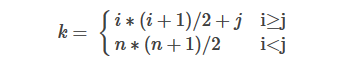5.1 数组的定义

在 C 语言中，一个二维数组类型可以定义为其分量类型为一维数组类型的一维数组类型，也就是说：

1
typedef elemtype array2[m][n];

等价于：

1
2
typedef elemtype array1[n];
typedef array1 array2[m];

数组一旦被定义，它的维数和维界就不再改变。因此，除了结构的初始化和销毁之外，数组只有存取元素和修改元素值的操作。

5.2 数组的存储方式

数组一般采用顺序存储，又分为行优先和列优先。数组的地址计算具有以下前提三要素：

  • 开始结点的存放地址（即基地址）。

  • 维数和每维的上、下界。

  • 每个数组元素所占用的单元数 L。

设一般的二维数组是A[c1…d1, c2…d2]，这里c1,c2不一定是0。

行优先存储时的地址公式为：LOC(aij)=LOC(c1,c2)+[(i-c1)*(d2-c2+1)+(j-c2)]*L。其中，c1,c2为数组基地址，i-c1为aij之前的行数，d2-c2+1为总列数，j-c2为aij本行前面元素个数，L为单个元素长度。

列优先存储的通式为：LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+(i-c1)]*L。

5.3 特殊矩阵

5.3.1 对称矩阵

（1）定义
在一个n阶方阵A中，若元素满足下述性质：aij=aji（0≤i, j≤n-1），即元素关于主对角线对称。

（2）存储方式

不失一般性，按“行优先顺序”存储主对角线以下元素，存储空间节省一半，如下所示：

a11
a21 a22
a31 a32 a33
…………………………
an1 an2 an3 …ann

在这个下三角矩阵中，ii 行 (0≤i<n)(0 ≤ i < n) 恰有 i+1i+1 个元素，矩阵元素总数为：1+2+...+n=n∗n+121+2+...+n = n * \frac{n+1}{2}，因此，可以按从上到下、从左到右将这些元素存放在一个向量 sa[0,...,n(n+1)2−1]sa[0, ... ,\frac {n(n+1)}{2}-1] 中。

若 i≥ji \geq j，则 aija_{ij} 在下三角矩阵中。aija_{ij} 之前的 ii 行(从第0行到第 i−1i-1 行)一共有 1+2+…+i=i * (i+1)/2 个元素，在第 ii 行上 aija_{ij} 之前恰有 jj 个元素(即 ai0，ai1，ai2，...，aij−1a_{i0}，a_{i1}，a_{i2}，...，a_{ij-1} )，因此：

k=i∗(i+1)2+j，0≤k<n(n+1)2k=\frac{i * (i+1)}{2} + j，0 \le k \lt \frac{n(n+1)}{2}

若 i<ji < j ，则 aija_{ij} 是在上三角矩阵中。因为 aij=ajia_{ij} = a_{ji} ，所以只要交换上述对应关系式中的 ii 和 jj 即可，得到：

k=j∗(j+1)2+i，0≤k<n(n+1)2k = \frac{j * (j+1)}{2} + i，0 \le k \lt \frac{n(n+1)}{2}

令 I=max(i,j),J=min(i,j)I=max(i,j), J=min(i,j) ,则 kk 和 i,ji,j 的对应关系统一为：

k=I∗(I+1)2+Jk = \frac{I \ast (I+1)}{2} + J

Loc(aij)=Loc(sa[k])=Loc(sa[0])+k∗dLoc(a_{ij}) = Loc(sa[k]) = Loc(sa[0]) + k \ast d

5.3.2 三角矩阵

（1）定义
以主对角线划分，三角矩阵有上三角和下三角。上三角矩阵：它的下三角(不包括主对角线)中的
元素均为常数。下三角矩阵正好相反，它的主对角线上方均为常数。在大多数情况下，三角矩阵常数为零。

（2）存储方式

  • 三角矩阵中的重复元素c可共享一个存储空间，其余的元素正好有n(n+1)/2个，因此，三角矩阵可压缩存储到向量sa[0..n(n+1)/2]中，其中c存放在向量的最后一个分量中。

  • 上三角矩阵：只存放上三角部分。a_{00} = sa[0], a_{01} = sa[1], a_{02} = sa[2], …，当 i≤ji \leq j 时，aija_{ij} 在上三角部分中，前面共有 i 行，共有n+n-1+n-2+…+n-(i-1) = i*n-i*(i-1)/2 = i*(2n-i+1)/2个元素，在第 i 行上，aija_{ij} 前恰好有 j−1j-1 个元素。sa[k]sa[k] 和 aija_{ij} 对应关系为：

上三角矩阵

  • 下三角矩阵的存储和对称矩阵用下三角存储类似，a00=sa[0],a10=sa[1],a11=sa[2],...a_{00} = sa[0], a_{10} = sa[1], a_{11} = sa[2],...， sa[k]sa[k] 和 aija_{ij} 对应关系为：

下三角矩阵

5.3.3 对角矩阵（三对角矩阵为例）

（1）定义
对角矩阵中，所有的非零元素集中在以主对角线为中心的带状区域中，即除了主对角线和主对角线相邻两侧的若干条对角线上的元素之外，其余元素皆为零。

（2）存储方式
非零元素仅出现在主对角线 (aij,0≤i≤n−1a_{ij}, 0 \leq i \leq n-1 )上，紧邻主对角线上面的那条对角线上( aij+1,0≤i≤n−2a_{ij+1}, 0 \leq i \leq n-2 )和紧邻主对角线下面的那条对角线上( ai+1,j,0≤i≤n−2a_{i+1,j}, 0 \leq i \leq n-2 )。显然，当| i-j |>1时，元素 aij=0a_{ij} = 0 。在一个n * n的三对角矩阵中，只有(n-1)+n+(n-1)个非零元素，故只需3n-2个存储单元，零元已不占用存储单元。

将n * n的三对角矩阵A压缩存放到只有3n-2个存储单元的sa向量中，假设仍按行优先顺序存放，则 sa[k]sa[k] 与 aija_{ij} 的对应关系为：

对角矩阵

在aij之前有i 行，共有3 x i-1个非零元素，在第 i 行，有j-i+1个非零元素，即非零元素aij的地址为： Loc(aij) = Loc(sa[k]) =LOC(0,0)+[3*i-1+(j-i+1)]*d=LOC(0,0)+(2*i+j)*d 。

5.4 稀疏矩阵及存储

5.4.1 概念

在实际应用中，经常会遇到另一类矩阵：其矩阵阶数很大，非零元个数较少，零元很多，且非零元的排列无规律可寻，则称这类矩阵为稀疏矩阵。

精确地说，设在的矩阵A中，有 s 个非零元。令 e = s / (m*n)，称 e 为矩阵 A 的稀疏因子。通常认为 e≤0.05e \le 0.05 时称矩阵 A 为稀疏矩阵。

稀疏矩阵由表示非零元的三元组及行列数唯一确定，一个三元组(i, j, aij)唯一确定了矩阵A的一个非零元。

例如：下列三元组表： ( (0,1,12), (0,2,9), (2,0,-3), (2,5,14), (3,2,24), (4,1,18), (5,0,15), (5,3,-7) )，加上(6,7,8) ——矩阵的行数、列数及非零元数便可作为矩阵M的另一种描述：

稀疏矩阵

5.4.2 三元组表表示法

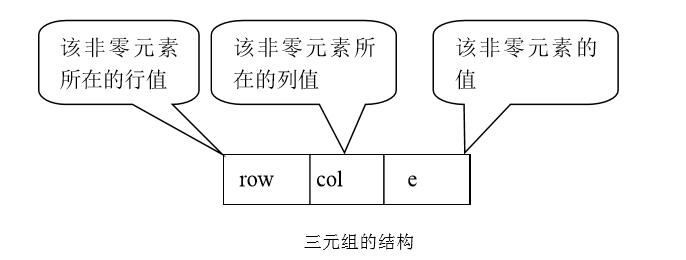
对于稀疏矩阵的压缩存储,采取只存储非零元素的方法。由于稀疏矩阵中非零元素 aij 的分布没有规律,因此,要求在存储非零元素值的同时还必须存储该非零元素在矩阵中所处的行号和列号的位置信息,这就是稀疏矩阵的三元组表表示法。

每个非零元素在一维数组中的表示形式如下图所示：

假设以顺序存储结构来表示三元组表，则可得到稀疏矩阵的一种压缩存储方法——三元顺序表。其定义如下：

1
2
3
4
5
6
7
8
9
10
11
#define maxsize 1000
typedef int datatype;
typedef struct {
    int i,j; 	/* 非零元的行、列下标 */
    datatype v; 	/* 元素值 */
} triplet;

typedef struct {
    triplet data[maxsize]; 	/* 三元组表 */
    int m,n,t; 	/* 行数、列数、非零元素个数 */
} tripletable; 	/* 稀疏矩阵类型 */

因此上面的三元组表的三元组顺序表表示如下：

i j v
0 1 12
0 2 9
2 0 -3
2 5 14
3 2 24
4 1 18
5 0 15
5 3 -7
M[0].i M[0].j M[0].t
6 6 8

显然，三元组顺序表存储会失去随机存取功能。

5.4.3 三元组顺序表的转置

一个 m×n 的矩阵 A，它的转置 B 是一个 n×m 的矩阵，且a[i][j]=b[j][i]，0 ≤ i < m，0 ≤ j < n，即A的行是B的列，A的列是B的行。

将A转置为 B，就是将 A 的三元组表 M[0].i 置换为表B的三元组表 M[0].i，如果只是简单地交换 a.data 中 i 和 j 的内容，那么得到的 b.data 将是一个M[0].i 顺序存储的稀疏矩阵 B，要得到按行优先顺序存储的 b.data，就必须 M[0].i 。

解决思路：只要做到：

  • 将矩阵行、列维数互换；
  • 将每个三元组中的i和j相互调换；
  • 重排三元组次序，使mb中元素以N的行(M的列)为主序。

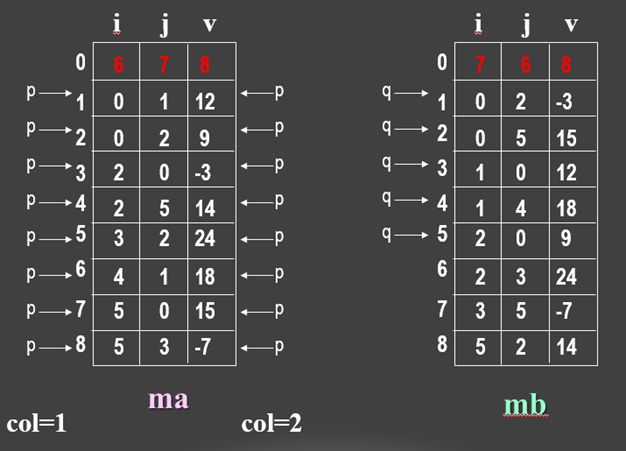
（1）方法一：按M的列序转置

即按 mb 中三元组次序依次在 ma 中找到相应的三元组进行转置。为找到M中每一列所有非零元素，需对其三元组表 ma 从第一行起扫描一遍。由于 ma 中以 M 行序为主序,所以由此得到的恰是 mb 中应有的顺序。

算法分析：T(n)=O(M的列数n * 非零元个数t )=O(n * t)，若 t 与m * n同数量级，则 T(n)=O(m∗n2)T(n)=O(m * n^2)。由此可见，进行转置运算时，虽然节省了存储单元，却大大增加了时间复杂度。

（2）方法二：快速转置

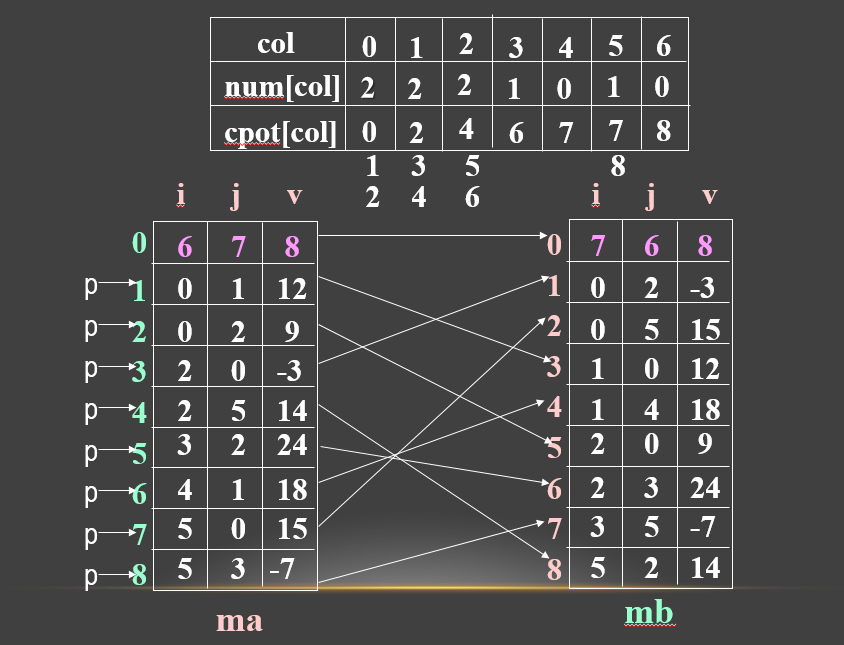
即按ma中三元组次序转置，转置结果放入mb中恰当位置。此法关键是要预先确定M中每一列第一个非零元在mb中位置，为确定这些位置，转置前应先求得M的每一列中非零元个数。

设两个数组：

  • num[col]：表示矩阵 M 中第 col 列中非零元个数。
  • cpot[col]：指示 M 中第 col 列第一个非零元在 mb 中的下标。

显然有：

1
2
cpot[0]=0; 
cpot[col]=cpot[col-1]+num[col-1];   (1<= col <= ma[0].j)

5.4.5 链式存储

（1）特点

  • 带行指针向量的单链表表示；

  • 每行的非零元用一个单链表存放；

  • 设置一个行指针数组，指向本行第一个非零元结点；若本行无非零元，则指针为空。

（2）表头结点与单链表结点类型定义

1
2
3
4
5
6
7
typedef struct node{ 
    int col;
    int val;
    struct node *link;
}JD;

typedef struct node *TD;

5.4.6 十字链表

与用二维数组存储稀疏矩阵相比较,用三元组表表示法的稀疏矩阵不仅节约了空间,而且 使得矩阵某些运算的时间效率优于经典算法。

但是当需进行矩阵加法、减法和乘法等运算时,有时矩阵中非零元素的位置和个数会发生很大的变化。如A =A+B,将矩阵 B 加到矩阵 A 上, 此时若用三元组表表示法,势必会为了保持三元组表“以行序为主序”而大量移动元素。

为了避免大量移动元素,介绍稀疏矩阵的链式存储法———十字链表,它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。

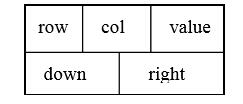
在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了(row,col,value)以外, 还要有以下两个链域:

  • right：用于链接同一行中的下一个非零元素。

  • down：用于链接同一列中的下一个非零元素。

在十字链表中,同一行的非零元素通过 right 域链接成一个单链表。同一列的非零元素通过 down 域链接成一个单链表。

这样,矩阵中任一非零元素 M[i][j] 所对应的结点既处在第i行的行链表上,又处在第j列的列链表上,这好像是处在一个十字交叉路口上,所以称其为十字链表。

同时再附设一个存放所有行链表的头指针的一维数组和一个存放所有列链表的头指针的一维数组。整个十字链表的结构如图所示。

十字链表的结点结构

十字链表的结构类型定义如下:

1
2
3
4
5
6
7
8
9
10
typedef struct OLNode { 
    int	row, col;        /*非零元素的行和列下标*/ 
    ElementType value; 
    struct OLNode *right, *down; /*非零元素所在行表、列表的后继链域*/ 
 }OLNode; *OLink; 

typedef struct { 
    OLink *row_head, *col_head;  /*行、列链表的头指针向量*/ 
    int	m, n, len;  /*稀疏矩阵的行数、列数、非零元素的个数*/  
 }CrossList;

5.5 广义表

广义表是线性表的推广。线性表中的元素仅限于原子项(单个数据元素)，即不可以再分，而广义表中的元素既可以是原子项，也可以是子表(另一个线性表)。 (如果ai是单个数据元素，则称ai为广义表的原子 )。

5.5.1 定义

广义表是n≥0个元素a0, a1, …, an-1的有限序列，其中每一个ai或者是原子，或者是一个广义表。

广义表通常记为GL=(a0,a1,…,an-1)，其中GL为广义表的名字，n为广义表的长度， 每一个ai为广义表的元素。一般用大写字母表示广义表，小写字母表示原子。

称第一个元素a0为广义表GL的表头，其余部分(a1,…an-1)为GL的表尾，分别记作：head(GL)=a0 ，tail(GL)=(a1,…an-1)。

5.5.2 说明

  • 广义表是线性表的一种推广。
  • 广义表的定义是递归的。因为在描述广义表的时候又用到了广义表的概念。
  • 广义表是多层次结构。
  • 一个广义表可以为其它广义表所共享。

5.5.3 举例

（1）A=( ), A为空表，长度为0。

（2）B=(a, (b,c))，B是长度为2的广义表，第一项为原子，第二项为广义表。

（3）

  • C=(x,y,z)，C是长度为3的广义表，每一项都是原子。
  • D=(B,C)，D是长度为2的广义表，每一项都是上面提到的广义表。
  • E=(a,E)，E是长度为2的广义表，第一项为原子，第二项为它本身。

5.5.4 广义表的深度

一个广义表的深度是指该广义表展开后所含括号的层数。

例如，A=(b,c)的深度为1， B=(A,d)的深度为2， C=(f,B,h)的深度为3。

5.5.5 取表头、表尾操作

（1）取表头
若广义表LS=(a1, a2, …, an)， 则head(LS)=a1 。取表头运算得到的结果可以是原子，也可以是一个子表。

例如：head((a1,a2,a3,a4))=a1 ，head(((a1,a2),(a3,a4),a5))=(a1,a2)。

（2）取表尾

若广义表LS=(a1, a2, …, an)，则tail(LS)=(a2, a3, …, an)。即取表尾运算得到的结果是除表头以外的所有元素，取表尾运算得到的结果一定是一个子表。

（3）注意
广义表( )和(())是不同的，前者为空表，长度为0，后者的长度为1，可得到表头、表尾均为空表，即: head((( )))=( )，tail((( )))=( )。

（4）举例
①. GetTail【(b, k, p, h)】＝ (k,p,h) ;

②. GetHead【( (a,b), (c,d) )】＝ (a,b) ;

③. GetTail【( (a,b), (c,d) )】＝ ((c,d)) ;

④. GetTail【 GetHead【((a,b),(c,d))】】＝ (b) ;

⑤. GetTail【(e)】＝ () ;

⑥. GetHead 【 ( ( ) )】＝ () ;

⑦. GetTail【 ( ( ) ) 】＝ () 。

5.6 广义表的存储结构

通常采用链接存储方法来存储广义表中元素，并称之为广义链表。

5.6.1 结点的表示

tag为标志字段。

  • 若tag=0 表示该结点为原子结点，第二个域data存放相应原子元素的信息。

  • 若tag=1为子表结点，第二个域为sublist存放相应子表第一个元素对应的结点的地址。

  • link存放本元素同一层的下一个元素所在链结点的地址。

C语言的定义如下：

1
2
3
4
5
6
7
8
typedef struct node {
    int tag;
    union {
        struct node *sublist;
        char data;
    } dd;
    struct node *link;
} NODE;

5.6.2 结点的链接

（1）一般的链接方法

广义表的每个元素有一个结点表示，同一层每个结点按其在表中的次序用link指针链接起来，每个表结点的sublist指向子表的第一个元素对应的结点。

（2）附加表头的链接方法

在每个广义表的表头结点之前增加一个表结点。相对于一般的链接方法，这种链接方法在进行元素的插入、删除和表的共享等处理时会显得更为方便。

5.7 例题

5.7.1 例1

数组A[0…6][0…8]的每个元素占5个单元，将其按列优先次序存储在起始地址为2000的连续内存单元中，则元素a[5][5]的地址为。

a[5][5] = 2000 + 5×[5×7+5] =2200

5.7.2 例2

二维数组A[0…4][0…4]的元素起始地址是LOC(A[0][0])=4000，每个元素占2个字节，则按行优先次序存储时LOC(A[3][3])为多少？

A[3][3] = 4000 + 2×(3×5+3) = 4036

5.7.3 例3

设三个广义表为：A=(a,b,©), B=(A,(c,d)), C=(a,(B,A),(e,f))。则 head[A]=_______，tail[B]=________。

head[head[head[tail[C]]]]=_______。

a ; ((c,d)) ; (a,b,©)